Человек решающий: интервью с членом задачного комитета Международной математической олимпиады Гезой Кошем
| Ксения Донская 27 сентября 2019 |
Вы вошли в состав жюри по математике Олимпиады мегаполисов. Какие у вас от нее впечатления?
Я бы сказал, что во многом она напоминает Международную математическую олимпиаду, сама система довольно похожая: соревнования идут два дня, на каждом туре дается по три задачи и 4,5 часа на их решение, в первые полчаса можно задавать вопросы по условиям, задания переведены на родные языки участников. На тех же университетских соревнованиях часто такого не бывает, нужно писать решение на официальном языке, чаще всего, на английском.
Геза Кош на церемонии закрытия IV Олимпиады мегаполисов
То есть, Мегаполисы могут стать хорошей разминкой перед Международной математической олимпиадой?
Конечно, и вообще, чем больше участвуешь в соревнованиях, тем лучше. Причем хорошо бы еще, чтобы они были международными. На национальном уровне довольно редко можно встретить такие сложные задания, как на Международной математической олимпиаде. А тут такая возможность есть. Еще я бы посоветовал соревнование Romanian Master of Mathematics, которое проходит в феврале, там тоже очень сложные задачи.
Расскажите, какие олимпиады проводятся в Венгрии?
У нас в стране математические соревнования имеют давнюю традицию. Старейшее из них организует журнал KöMaL, ему около 125 лет: на время двух мировых войн его выпуск приостанавливали, а после возобновляли. Среди участников этой олимпиады немало всемирно известных ученых, например, Липот Фейер или Пал Эрдёш.
В течение учебного года журнал каждый месяц публикует задачи по физике, математике и информатике. Их, кстати, можно найти в интернете, в том числе, на английском языке. После этого у детей есть месяц, чтобы выслать нам свои решения по почте или в электронном виде. Затем мы приступаем к проверке. У нас много помощников, в основном, студентов, без них мы бы не справились: участников очень много. Финальные результаты публикуются в конце июля.
А кто придумывает задания для этой олимпиады?
Внутри редакции работают несколько комиссий, я состою в двух из них. И мы постоянно отбираем новые задания: что-то сами придумываем, что-то читатели присылают. Бывает и такое, что мы берем старые задачи и обязательно как-то их меняем. Без этого никак: иначе дети просто найдут решения в интернете. Так что сейчас подобные дистанционные соревнования, конечно, довольно сложно проводить.
А какие-нибудь большие очные олимпиады вроде нашей Всероссийской у вас есть?
У нас есть олимпиада имени Йожефа Кюршака, она проводится в 20 городах. В Венгрии живут около 10 миллионов человек – меньше, чем в Москве. Кто-то из наших соотечественников переезжает в Румынию, Словакию, Сербию, но они тоже могут участвовать в таких соревнованиях.
Как думаете, можно ли сказать, что в Венгрии олимпиады пользуются популярностью?
Пожалуй, да. В заочной олимпиаде журнала KöMaL, например, участвует больше 1200 человек. И призы тут, как правило, второстепенны: главный плюс таких соревнований – это практика. Она очень всем пригодится в университете. Потому что там учеба идет в совершенно другом темпе, и если ты не привык регулярно усердно работать, велик риск не справиться с напряжением.
Венгрия хорошо выступает на Международной математической олимпиаде, вы никогда не остаетесь без медалей. Как к ней готовят учащихся?
Во-первых, они постоянно тренируются на заданиях из журнала. Кроме того, проводятся специальные соревнования, чтобы отобрать ребят в сборную. А перед самой олимпиадой у них трехнедельные сборы в лагере.
Я знаю, что вас с Международной математической олимпиадой связывает долгая история: у вас серебро и два золота, при этом вы дважды стали абсолютным победителем...
Да, но в те годы были и другие абсолютные, мы набрали одинаковое число баллов!
И тем не менее! Как вам кажется, меняется ли олимпиада со временем? Становится ли соперничество более жестким?
Меняется уровень заданий. У сильнейших команд сегодня более серьезная подготовка, чем во времена моей учебы, поэтому и задачи должны быть гораздо труднее. С другой стороны, со временем появляются новые страны-участники, и для них нужны задачи попроще.
Участники IV Олимпиады мегаполисов на втором туре по математике
Чтобы у школьников из только присоединившихся стран было ощущение, что у них тоже что-то получилось?
Kонечно! Нельзя же отправлять половину ребят домой с нулем баллов. Таким образом, диапазон сложности заданий за последние годы сильно расширился: первые задачи стали проще, а последние – сложнее.
Также более профессиональной стала система отбора заданий. Раньше, насколько мне известно, сами члены жюри приносили какие-то задачи, из них и составляли олимпиаду. А сейчас есть специальный комитет, который занимается отбором, я тоже в него вхожу. В этом году нам прислали больше 200 задач. Мы сразу отказались от тех, которые где-то публиковались прежде, а дальше уже смотрели по критериям. Если задача слишком простая или слишком сложная, если решение недостаточно элегантное, то она, конечно, в финальный список не попадет. В каких-то заданиях пришлось перефразировать условия, потому что формулировки были сыроваты. В итоге мы составили шорт-лист самых интересных заданий и отправили его жюри.
Как вы думаете, ваш олимпиадный опыт помогает вам готовить новых победителей? Может, у вас есть какие-то лайфхаки для будущих участников?
Думаю, да, во многом это идет на пользу. Во-первых, если хочешь показать детям, как решать какую-то задачу, нужно ведь и самому в ней разобраться. И здорово, что я могу делиться с ними своим опытом участия в соревнованиях.
Мне кажется, важно помнить, что после всех олимпиад и выпуска из школы начинается совершенно новая жизнь. Конечно, здорово, когда у тебя есть такая внушительная подготовка, хорошо, что ты умеешь быстро решать сложные задачи, но в научной деятельности часто требуется совсем другое. Так что надо понимать, что игры кончились и надо чем-то реальным заниматься.
Да, получается, для олимпиад и тех же исследований, например, часто важны разные качества: в соревнованиях ценится скорость и умение быстро концентрироваться, а в науке ты можешь долго-долго трудиться над чем-то одним.
Это правда, в вопросах скорости тут все совсем по-разному. На Международной математической олимпиаде нужно несколько часов быть чрезвычайно быстрым, а в исследованиях так гнать просто невозможно: они порой требуют месяцев кропотливой работы.
Вы сами придумываете олимпиадные задачи. Любопытно было бы узнать, как проходит этот процесс?
Мне кажется, это что-то сродни вопросу «Как писать музыку?» На самом деле, придумывать задачи гораздо сложнее, чем решать их.
Нужно вдохновение?
Конечно! Нужны новые идеи. Вы можете что-то где-то заметить и прикинуть, нельзя ли это «что-то» использовать в новой задаче. Мне кажется, примерно так же придумываются головоломки. Например, около 20 лет назад я увидел в Лондоне очень интересную классическую головоломку и сначала решил ее просто перебором вариантов, а потом уже понял, по каким принципам там все устроено. И мне она показалась настолько любопытной, что я ее усовершенствовал и создал еще более сложную версию.
Фото головоломки с соцсети Гезы КошаСуть в том, что вам нужно снять кольцо. Сделать это очень трудно, обычно все радуются, даже если получилось хотя бы чуть-чуть продвинуться вперед. Кто-то и вовсе говорит, что это нереально. А я как раз люблю такие головоломки на грани возможного, люблю сам что-то подобное решать и других озадачивать!
Как вам кажется, подобные головоломки скорее полезны для тех, кто только начинает интересоваться математикой, или опытным олимпиадникам тоже пригодятся?
Олимпиады и головоломки – это, конечно, разные вещи, но нам важно показать детям, что думать над задачами интересно, помочь им ощутить, какая это радость – что-то решить. И тут как раз очень помогают головоломки.
Иногда людям кажется, что математика вся состоит из каких-то страшных формул на доске, но это же просто язык, с помощью которого ты описываешь какие-то процессы. Головоломки как раз помогают почувствовать себя первооткрывателем, испытать восторг, когда разгадка все же найдена.
Первый шаг к тому, чтобы заинтересоваться математикой, это найти какие-то задачи, которые будут вас радовать.
Бывает, люди говорят, что у них нет способностей к математике. Вы верите, что такое действительно бывает?
Тут дело совсем не в математике, а в психологии: иногда люди просто сдаются. Возможно, в младшей школе у них как-то не очень удачно все пошло, и они из этого делают вывод, что их мозг математику не воспринимает. Конечно, это далеко на всегда становится проблемой: в повседневной жизни нам не нужно ежедневно решать дифференциальные уравнения.
И тем не менее, как показать, что математика не скучная и что ничего страшного в ней нет?
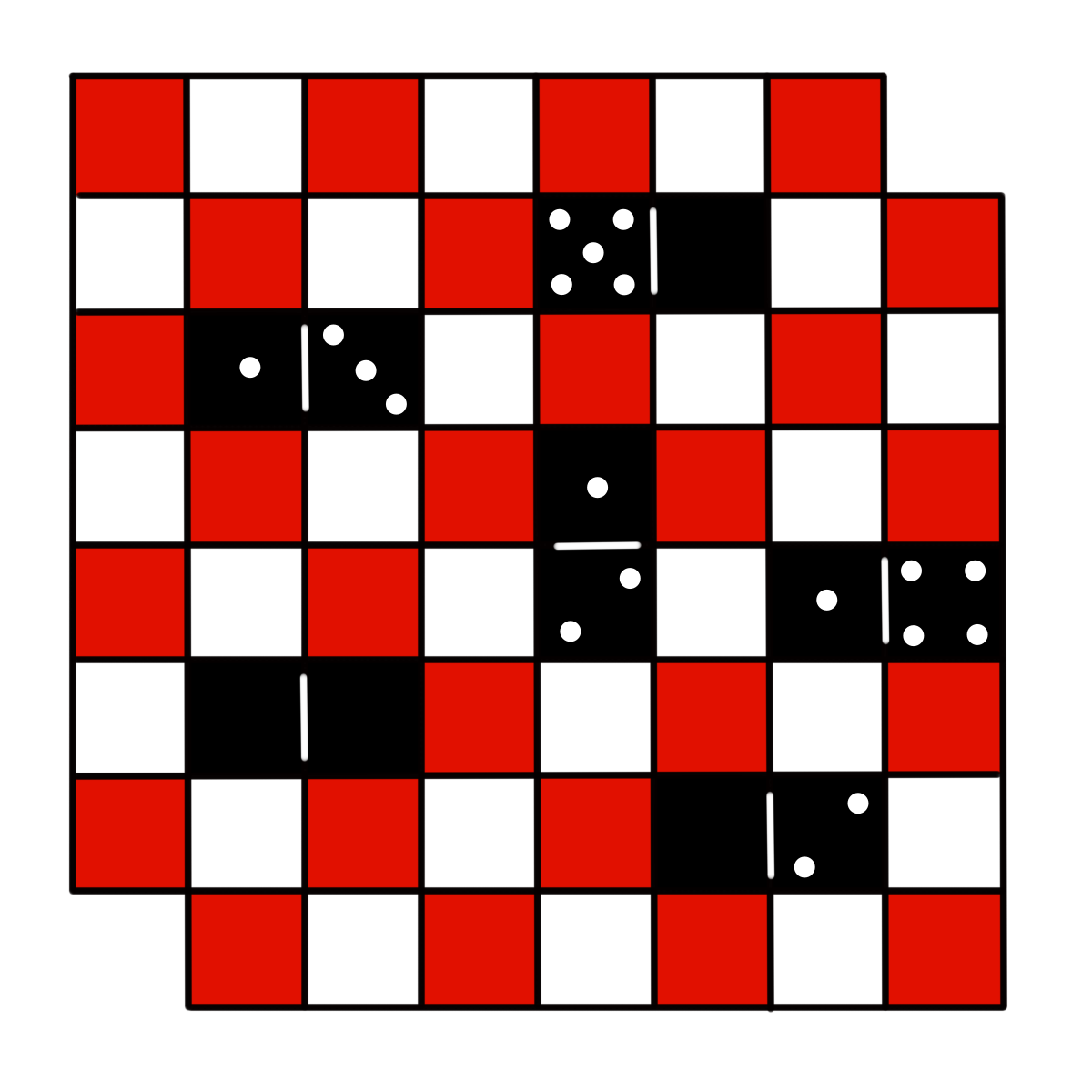
Тут опять же помогают головоломки и задачи с изюминкой. Например, несколько недель назад я встретил человека, который ровно это и твердил: «Математика не для меня, ничего в ней не понимаю». Я показал ему классическую математическую головоломку: из шахматного поля вырезаны два противоположных угла, и нам нужно его полностью замостить домино, причем каждая фишка закрывает две соседние клетки. Вопрос в том, как это сделать и реально ли это вообще? Ответ: нереально, ведь каждая фишка закрывает черную и белую клетку, а поскольку в вырезанных углах у нас были клетки одного цвета, баланс черного и белого нарушен. В подобных задачах люди часто начинают перебирать разные варианты, но это, конечно, не доказательство. Вот и мой новый знакомый решение найти не смог, но головоломка его увлекла. А ведь заданий на раскрашивание и разрезание великое множество! Поэтому первый шаг к тому, чтобы заинтересоваться математикой, это найти какие-то задачи, которые будут вас радовать.
Математическая головоломкаЕще бывает так, что во время изучения математики люди пропускают какую-то одну ступеньку, и в результате это им аукается. Например, один мой друг попросил меня позаниматься с его двенадцатилетней дочерью: ей никак не давались расчеты с процентами. Мы попробовали решить несколько задач, и действительно, у нее ничего не получалось. Тогда я перешел к заданиям попроще, и тут оказалось, что девочка не умеет складывать дроби! Она не поняла эту тему три года назад! Мы во всем разобрались, больше никаких проблем у нее не возникало, родители были счастливы. Это я к тому, что нам может не хватать каких-то знаний, до поры до времени мы закрываем на это глаза, но в итоге это может привести к печальному финалу. И если таким людям не помочь, не восполнить их пробелы, они так и будут думать, что у них нет способностей.
На какие соревнования вы бы посоветовали обратить внимание ребятам, которые увлекаются математикой?
Старшеклассникам я бы все-таки посоветовал олимпиаду, которую проводит журнал KöMaL. Знаю, что у вас есть «Квант» и «Квантик», наверняка там тоже существует нечто подобное.